Classificação usando KNN

Na tarefa de classificação estamos procurando por um modelo (algoritmo) que melhor consiga definir a classe (rótulo) dos dados.
Exemplos:
- Classificar se um email é spam ou não;
- Classificar a área responsável ou urgência para atender um chamado;
- Classificar se um produto ou software é bom de acordo com a quantidade de problemas ou vendas;
Existem diversos algoritmos capazes de realizar essa tarefa, neste artigo veremos o algoritmo K-Nearest Neighbors (K vizinhos mais próximo), que utiliza uma medida de distância entre as amostras para definir a qual classe uma nova amostra pertence.
K-Nearest Neighbors (KNN)
Quando queremos realizar a tarefa de classificação, precisamos de um dataset contendo as características que serão utilizadas no treinamento do modelo. As características são normalmente convertidas e normalizadas para números na etapa de pré processamento (vou escrever outro artigo só sobre isso).
Na montagem do dataset também identificamos a qual classe cada amostra pertence. Exemplo de um dataset simples, no qual temos duas características x e y que serão usadas para aprender a definir qual classe (classificação) 0 ou 1 esses valores representam:
| x | y | classe |
|---|---|---|
| 7 | 30 | 1 |
| 8 | 30 | 1 |
| 3 | 20 | 0 |
| 6 | 60 | 1 |
| 5.5 | 35 | 0 |
| 8 | 50 | 1 |
| 8 | 60 | 1 |
| 2 | 70 | 0 |
| 3 | 40 | 0 |
| 9 | 60 | 1 |
| 6 | 30 | 0 |
| 3 | 90 | 0 |
| 3 | 60 | 0 |
| 7 | 20 | 1 |
| 5 | 40 | 0 |
| 7 | 70 | 1 |
Obs: para facilitar o exemplo estou usando só duas características x e y (imagine que as características são as informações que representam os dados que serão classificados) e duas classes 0 e 1 (imagine as possíveis classificações que essas características podem representar), mas na prática os problemas possuem muito mais características. Outro ponto importante é que estou usando valores numéricos para representar os valores das características e possíveis classificações.
Na Figura 1 apresento visualmente os dados desse dataset. É sempre interessante tentar visualizar os dados para ver como se distribuem, nesse exemplo consigo fazer essa representação facilmente porque tenho apenas duas características, se tivesse mais características o ideal é escolher duas ou três que melhor representam os dados para fazer sua visualização gráfica.
Figura 1: Visualizando os dados.
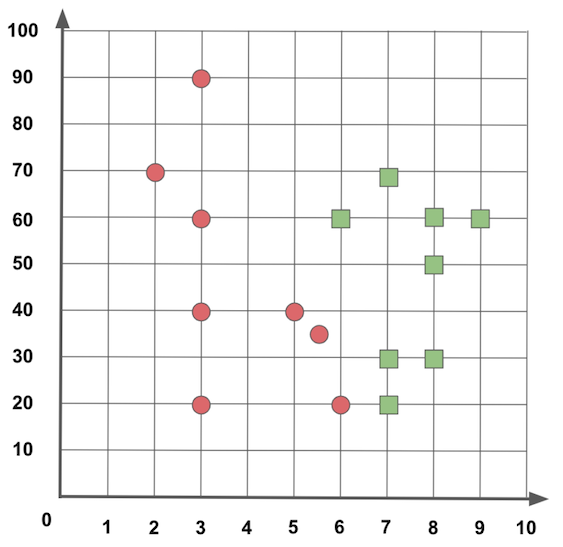
Como as amostras usadas para montar o dataset inicial foram previamente classificadas, então sei quais dados representam o Círculo Vermelho ou o valor 0, e quais dados representam o Quadrado Verde ou o valor 1, dizemos que o KNN utiliza um treinamento supervisionado, porque teve a ajuda de um especialista para identificar as classificações de cada amostra.
A partir do momento que temos o dataset com as características no formato numérico, o KNN funcionará da seguinte maneira: 1- calcula a distância entre uma nova amostra e as demais amostras do dataset (imagine algo como a distância entre dois pontos no plano cartesiano, mas logo a seguir comento sobre isso); 2- identifica as K amostras mais próximas ou com características mais similares (depois que você tem o valor da distância, é só escolher as K distâncias com os menores valores); 3- a partir das K amostras mais próximas, verificamos qual o rótulo que mais aparece e esse rótulo será usado na nova amostra.
No exemplo apresentado na Figura 2 temos duas classificações possíveis, você pode imaginar, por exemplo, que a classe Quadrado Verde significa que um email é spam e a classe Circulo Vermelho significa que um email não é spam. Agora recebemos um novo email (nova amostra) sinalizada pelo Triângulo Azul que queremos classificar se é spam ou não spam.
Usando o algoritmo do KNN vamos primeiro definir como calcular o quão similar são dois emails, nesse exemplo, hipoteticamente imagine que foi escolhido duas palavras no título do email, que são representadas por números e indicam se é spam ou não é spam. Aqui estou usando somente duas palavras para representar no espaço bidimensional e mostrar graficamente nas figuras a seguir, mas tenha em mente que em um caso real serão várias palavras que te ajudaram a realizar essa classificação.
Então digamos que temos uma função que mede distância entre duas amostras, como a Distância Euclidiana, na qual os valores das características de cada amostra vai calcular e devolver um valor representando essa distância. O K do KNN indica o número de vizinhos mais próximos de uma amostra que serão usados para identificar o tipo desta amostra. Na Figura 2 estamos usando K = 3 para indicar que queremos usar os três vizinhos mais próximos.
Figura 2: Distância entre três amostras mais próximas.
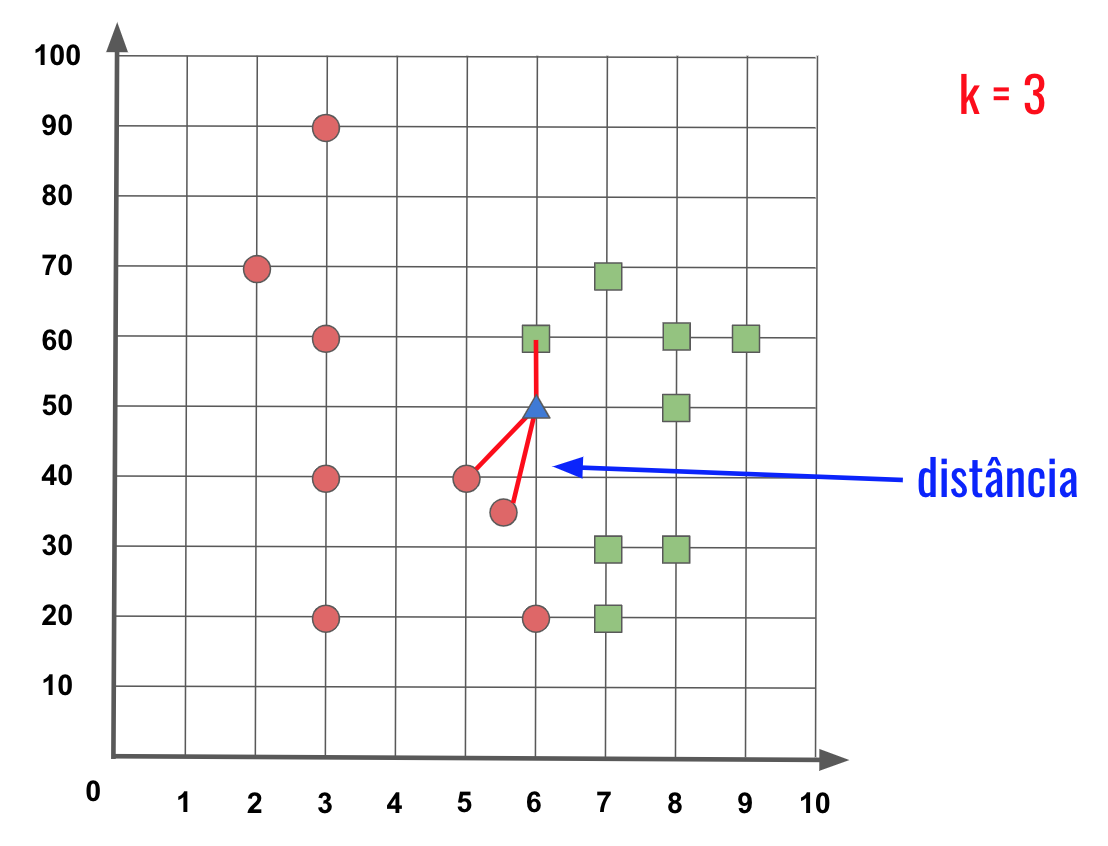
Olhando esses três vizinhos mais próximos, podemos ver que duas amostras são Círculos Vermelhos e apenas uma amostra é Quadrado Verde, então pela maioria podemos dizer que a nova amostra no Triângulo Azul é na verdade da classe do Círculo Vermelho.
Um ponto interessante é que quando temos apenas duas classes, você pode usar um valor ímpar para o K, assim evita um empate entre as possíveis classes mais próximas.
Mas agora se usarmos o K = 5, podemos ver na Figura 3 que entre as amostras mais próximas, temos duas amostras que são Círculos Vermelhos e três amostras que são Quadrados Verdes, então a nova amostra do Triângulo Azul é na verdade da classe do Quadrado Verde.
Figura 3: Distância entre cinco amostras mais próximas.
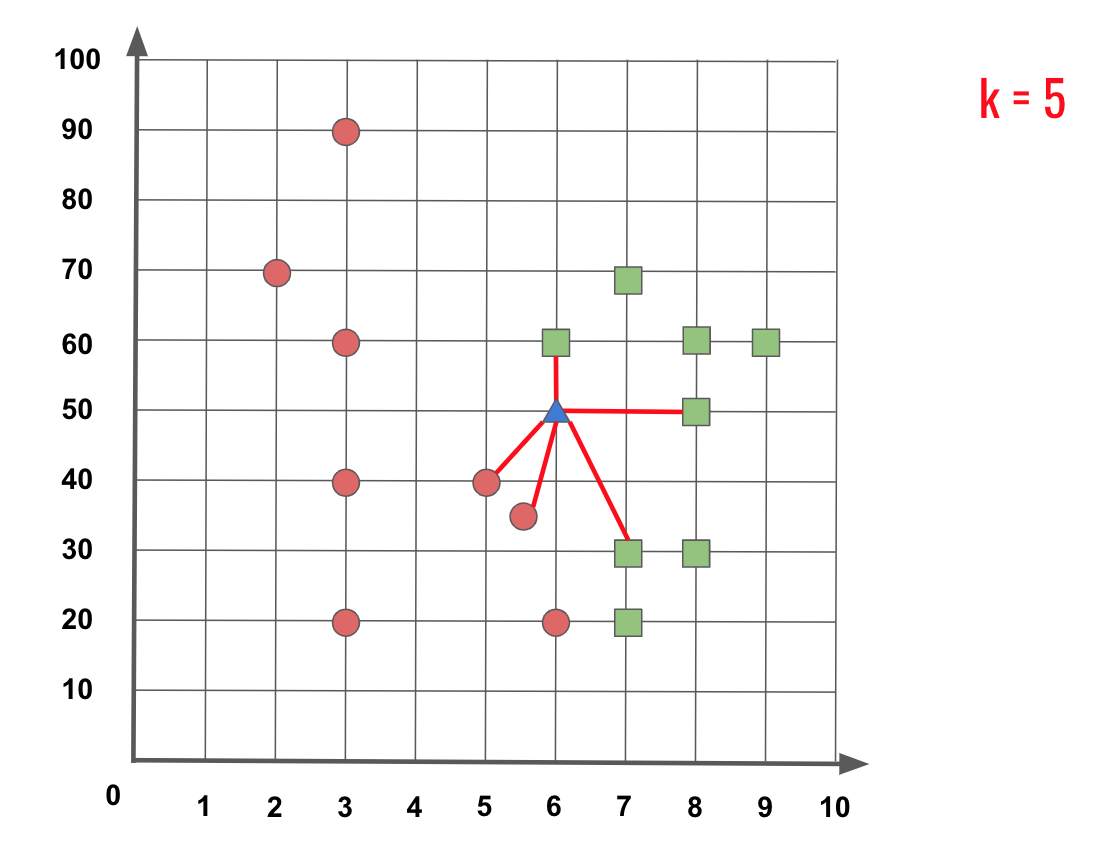
Mas agora você deve estar perguntando, qual valor utilizar para o K?
Como o K influencia na classificação das novas amostras, realizamos o treino do KNN com valores diferentes de K, assim conseguimos verificar com base nas amostras de exemplo qual o valor de K que melhor representa a classificação.
Durante o treinamento separamos uma parte do dataset para treino e outra parte para teste, também definimos um valor para K, então 1) usamos a parte do treino como os dados que o KNN conhece para gerar a classificação das novas amostras; e 2) usamos os dados de teste para verificar o quanto o KNN acertou e errou a classificação com base no tamanho do K informado. Assim geramos uma medida de desempenho para cada K. Então teste o K com valores variados: 10, 100, 1000 (lembrando que essa quantidade tem que ser menor que o total de amostras do dataset).
Além do valor de K, outro ponto que influencia muito a classificação é a função utilizada para calcular a distância entre os exemplos, porque o resultado desta função vai dizer o quão similar são duas amostras. Veremos a seguir alguns exemplos de distâncias que podem ser usadas pelo KNN.
Distâncias
Para determinar quais amostras são vizinhas uma da outra, é necessário utilizar alguma medida de distância. Essa distância mede a similaridade entre duas amostras. Quando o resultado da função é um valor baixo, indica que duas amostras estão próximas, por tanto são mais similares; e quando o valor é alto, indica que duas amostras estão longes, por tanto não são similares.
A seguir temos o exemplo de algumas funções de distâncias usadas para medir a similaridade entre as amostras.
Distância de Manhattan
A distância de Manhattan vem da ideia de calcular a distância de quarteirões que devem ser percorridos por um carro entre dois locais na cidade de Manhattan.
A Figura 4 apresenta a função da distância Manhattan. A distância é calculada somando o valor absoluto da diferença entre cada característica, por isso que na fórmula tem essa somatória de i começando em zero, até i igual a n (quantidade de características) - 1, a e b são duas amostras que queremos calcular a similaridade e representam o vetor de características de cada amostra. Podemos imaginar que cada característica representa um quarteirão ou uma reta, e no final queremos somar todos quarteirões para descobrir o total que será percorrido.
Figura 4: função da distância de Manhattan.
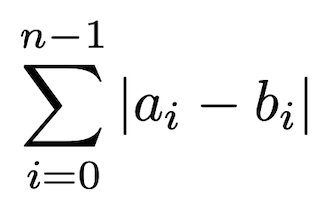
Então essa função calcula a distância como a soma de várias retas na horizontal e vertical, simulando o caminho que um carro percorre pelos quarteirões.
Distância Euclidiana
A distância Euclidiana é similar a distância de Manhattan. Para não ter um resultado com valor negativo, a diferença entre a mesma característica de cada amostra é elevada ao quadrado, e no final da somatória é calculado a raiz quadrada, é como se ao invés de somar as retas dos quarteirões, queremos traçar um caminho reto entre as duas amostras.
A Figura 5 apresenta a função da distância Euclidiana.
Figura 5: função da distância Euclidiana.
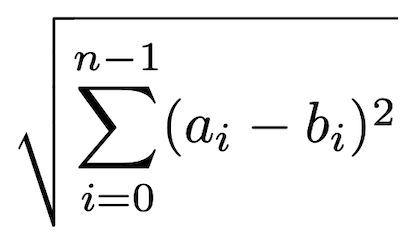
Na Figura 6, temos os caminhos em vermelho, azul e amarelo que representam soluções geradas pela distância de Manhattan e a linha verde é o caminho gerado pela distância Euclidiana.
Figura 6: diferença entre distância Manhattan e Euclidiana.

Distância de Minkowski
A distância de Minkowski é considerada uma generalização das distância de Manhattan e Euclidiana.
Figura 7: função da Distância Minkowski.
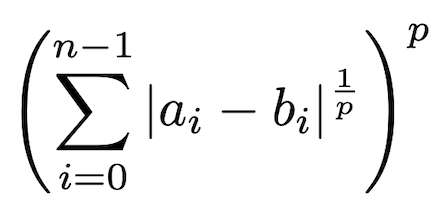
Se o valor de p for igual a 1, então o resultado é o mesmo da distância de Manhattan e se o valor de p for igual a 2, então o resultado é o mesmo da distância Euclidiana.
Distância Levenshtein ou Distância de Edição
A distância Levenshtein é usada para calcular quantos caracteres precisam ser alterado para ir de um texto até outro texto, por isso que também é chamada de distância de edição.
Utilizando o KNN para classificar as flores íris
Vamos fazer um novo exemplo usando o Iris Dataset que é composto por cinco características: SepalLength (Comprimento da Sépala), SepalWidth (Largura da Sépala), PetalLength (Comprimento da Pétala), PetalWidth (Largura da Pétala) e Class (Classe).
A seguir temos algumas linhas deste dataset:
| SepalLength | SepalWidth | PetalLength | PetalWidth | Class |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | Iris-setosa |
| 5.0 | 3.3 | 1.4 | 0.2 | Iris-setosa |
| 7.0 | 3.2 | 4.7 | 1.4 | Iris-versicolor |
| 5.7 | 2.8 | 4.1 | 1.3 | Iris-versicolor |
| 6.3 | 3.3 | 6.0 | 2.5 | Iris-virginica |
| 5.9 | 3.0 | 5.1 | 1.8 | Iris-virginica |
Existem três classes Versicolor, Setosa e Virginica, e com base nas características da flor queremos identificar a qual classe ela pertence.
Figura 8: tipos de flores Íris.

Vou mostrar a seguir como carregar e treinar esse modelo usando Java e Python, o resultado final é bem similar, mas serve como comparativo entre as duas linguagens.
Carregando o dataset
Vamos iniciar carregando os dados que estão no Iris Dataset, esse arquivo contém 100 exemplos e seus dados estão separados por vírgula.
Carregando o dataset em Java
A biblioteca Smile possui uma implementação em Java do KNN, para usá-lo no seu projeto, você pode fazer download do projeto no Github ou adicionar a dependência Maven no pom.xml:
1
2
3
4
5
6
7
8
9
10
11
<dependency>
<groupId>com.github.haifengl</groupId>
<artifactId>smile-core</artifactId>
<version>2.0.0</version>
</dependency>
<dependency>
<groupId>com.github.haifengl</groupId>
<artifactId>smile-io</artifactId>
<version>2.3.0</version>
</dependency>
Depois de adicionar a dependência no projeto, vamos carregar os dados. Criei um formato do CSV para definir o cabeçalho, porque esse arquivo não possui cabeçalho, depois carreguei o DataFrame a partir do arquivo iris.data e criei uma escala para a coluna “Class” que representa os três tipos de rótulos para as flores Iris.
A partir do DataFrame, selecionei as colunas com as características serão usadas no treino do KNN e guardei na matrix X e também peguei a coluna “Class”, mas primeiro converti ela para a escala numerica e guardei no vetor y.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import org.apache.commons.csv.CSVFormat;
import smile.data.DataFrame;
import smile.data.measure.NominalScale;
import smile.io.CSV;
public class Classificador {
public static void main(String[] args) throws Exception {
CSVFormat format = CSVFormat.DEFAULT.withHeader("SepalLength", "SepalWidth", "PetalLength", "PetalWidth", "Class");
DataFrame df = new CSV(format).read("iris.data");
NominalScale nominalScale = df.stringVector("Class").nominal();
double[][] X = df.select("SepalLength", "SepalWidth", "PetalLength", "PetalWidth").toArray();
int[] y = df.stringVector("Class").factorize(nominalScale).toIntArray();
}
}
Observação: quando você for executar esse código no seu computador, verifique se o caminho do arquivo iris.data está correto.
Carregando o dataset em Python
Para carregar os dados das flores Iris em Python, vou usar o Pandas para ajudar. Neste código importei o Pandas, informei o nome das características do dataset (porque esse arquivo não tem cabeçalho), li o CSV e separei em duas variáveis, sendo X uma matriz com as características e y um vetor com as classes:
1
2
3
4
5
6
import pandas as pd
nomes = ['SepalLength', 'SepalWidth', 'PetalLength', 'PetalWidth', 'Class']
df = pd.read_csv('iris.data', names = nomes)
X = df[df.columns.difference(['Class'])].values
y = df['Class'].values
Treinando o KNN
Conseguimos ler os dados do dataset e guardamos as características na matriz X e as classes no vetor y, agora vamos usar esses dados para treinar o KNN.
Treinando o KNN em Java
Altere a classe Classificador para treina o KNN após carregar os dados:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import java.util.Arrays;
import org.apache.commons.csv.CSVFormat;
import smile.classification.KNN;
import smile.data.DataFrame;
import smile.data.measure.NominalScale;
import smile.io.CSV;
import smile.math.distance.EuclideanDistance;
import smile.neighbor.CoverTree;
import smile.neighbor.KNNSearch;
public class Classificador {
public static void main(String[] args) throws Exception {
CSVFormat format = CSVFormat.DEFAULT.withHeader("SepalLength", "SepalWidth", "PetalLength", "PetalWidth", "Class");
DataFrame df = new CSV(format).read("iris.data");
NominalScale nominalScale = df.stringVector("Class").nominal();
double[][] X = df.select("SepalLength", "SepalWidth", "PetalLength", "PetalWidth").toArray();
int[] y = df.stringVector("Class").factorize(nominalScale).toIntArray();
int k = 3;
KNNSearch search = new CoverTree(X, new EuclideanDistance());
KNN knn = new KNN(search, y, k);
}
}
Nesse código estamos instanciando o algoritmo do KNN usando a distância Euclidiana para calcular a distância das características das flores que foi passada na variável X. Também passei o vetor y com as classificações esperadas e o valor do k (nesse exemplo usei k = 3).
Quando instanciamos o KNN, nesse momento ocorre o treino do modelo com base nos dados passados.
Treinando o KNN em Python
Para treinar o KNN em Python, vou usar a implementação do Scikit:
1
2
3
4
from sklearn.neighbors import KNeighborsClassifier
iris_classificador = KNeighborsClassifier(n_neighbors = 3)
iris_classificador.fit(X, y)
Importei o KNeighborsClassifier que é uma implementação do KNN, configurei o n_neighbors (que representa o tamanho do k vizinhos) com 3 e depois chamei o método fit para treinar o modelo. A implementação padrão usada para calcular a distância é o inverso da função de Minkowski, por tanto um número grande representa uma similaridade maior e um número pequeno representa uma similaridade menor.
Avaliando o desempenho do KNN
Usamos uma implementação pronta do KNN, mas qual o valor de K que devemos usar?
Uma das formas é testando o KNN com vários K diferentes. Podemos usar a validação cruzada para avaliar o desempenho do KNN para cada K que escolhemos.
A validação cruzada divide seu dataset em partes, então se escolhermos, por exemplo, dividir esse dataset que possui 100 amostras em 5, teremos 5 partes com 20 amostras escolhidas aleatoriamente.
A validação cruzada vai separar uma dessas partes contendo 20 amostras e treinar o KNN com o restante.
Após o treino, utiliza a parte separada para avaliar como está a classificação feita pelo KNN.
Avaliando o desempenho do KNN em Python
Avaliando o desempenho do KNN com validação cruzada:
1
2
3
4
from sklearn.model_selection import cross_val_score
scores_dt = cross_val_score(iris_classificador, X, y, scoring='accuracy', cv=5)
print(scores_dt.mean())
Saída:
1
0.9800000000000001
O cross_val_score é uma implementação da validação cruzada, que recebe como parâmetro o conjunto de dados de entrada X, um vetor com as saídas esperadas y, o nome da funcao
Executei a validação cruzada para K de 1 até 10:
Figura 9: Resultado da avaliação cruzada para K de 1 até 10.
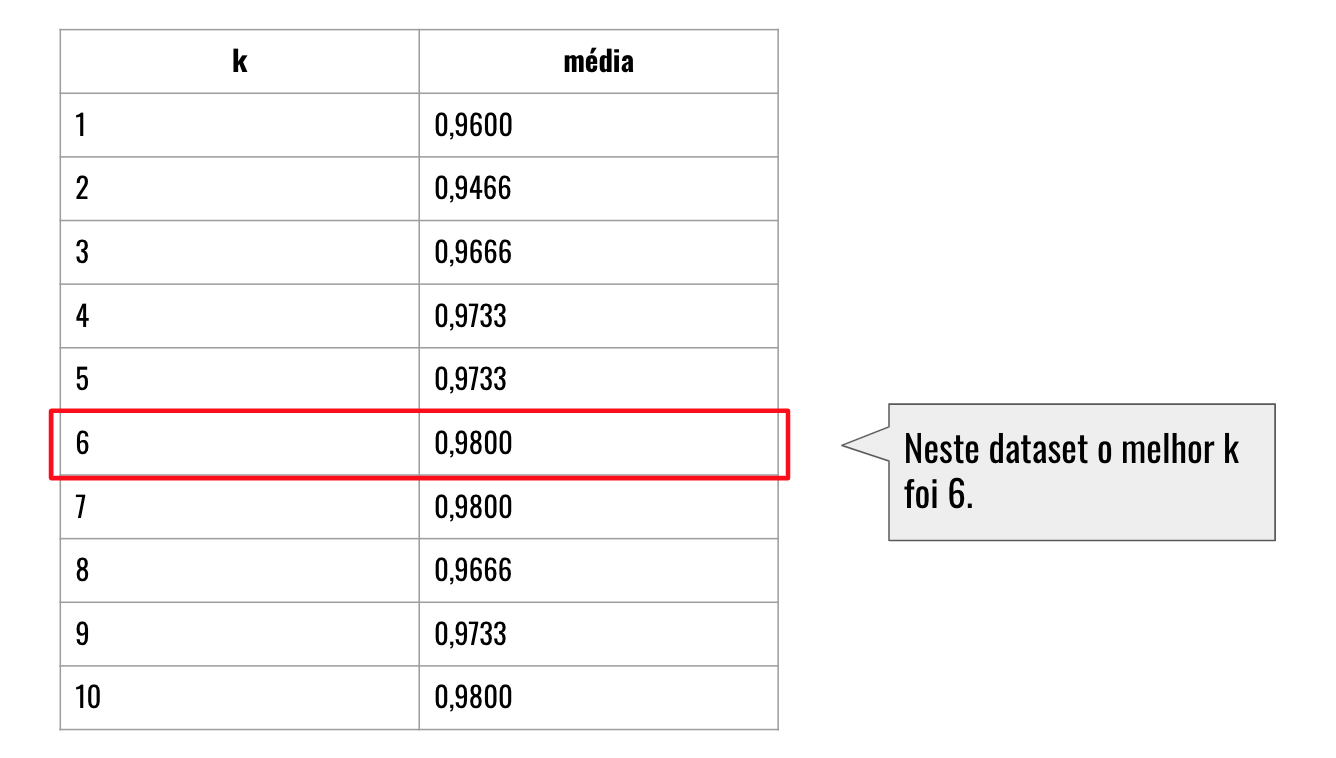
Neste dataset e testando os intervalos de 1 até 10, o melhor KNN treinado foi utilizando K = 6. Então para as amostras usadas para testar o KNN, foram usadas as seis amostras com menor distância para definir a qual classe cada uma das amostras pertence.
Mas você pode querer perguntar: porque o K = 6 é o melhor, sendo que o K = 7 e o K = 10 também conseguiram a mesma média de 0,9800? A resposta é porque o K = 6 precisa de menos comparações para realizar a classificação, então usa apenas as 6 amostras mais próximas para determinar a classificação de uma nova amostra.
Predizendo a classe de novas amostras
Realizei o treinamento usando todo o dataset para treinar o KNN e com o valor de K = 6. Agora peguei as medidas de mais três novas amostras para classificar.
| SepalLength | SepalWidth | PetalLength | PetalWidth | Class |
|---|---|---|---|---|
| 5.0 | 3.6 | 1.6 | 0.5 | ? |
| 5.8 | 2.7 | 4.2 | 1.2 | ? |
| 7.0 | 3.2 | 5.2 | 2.4 | ? |
A qual classe pertence cada uma dessas amostras?
Avaliando novas amostras em Java
A implementação do KNN possui o método predict que recebe como parâmetro um vetor de características e devolve o número da classe que ele classificou esses dados.
Altere a classe Classificador e inclui após o treinamento alguns novos exemplos para ver como o KNN vai classificá-los:
1
2
3
4
5
6
7
8
9
double[][] novos_exemplos = new double[][]{
{5.0, 3.6, 1.6, 0.5},
{5.8, 2.7, 4.2, 1.2},
{7.0, 3.2, 5.2, 2.4}
};
for (double[] novo : novos_exemplos) {
int predicao = knn.predict(novo);
System.out.println(Arrays.toString(novo) + " = " + nominalScale.level(predicao));
}
Saída:
1
2
3
[5.0, 3.6, 1.6, 0.5] = Iris-setosa
[5.8, 2.7, 4.2, 1.2] = Iris-versicolor
[7.0, 3.2, 5.2, 2.4] = Iris-virginica
Avaliando novas amostras em Python
Para classificar usando a implementação do KNN em Python:
1
2
3
4
novos_exemplos = [[1.6,0.5,5.0,3.6],
[4.2,1.2,5.8,2.7],
[5.2,2.4,7.0,3.2]]
print(iris_classificador.predict(novos_exemplos))
O KNeighborsClassifier possui o método predict, que recebe uma ou mais amostras para ele classificar e sua saída é um vetor com as classificações.
1
['Iris-setosa' 'Iris-versicolor' 'Iris-virginica']